문제 : https://www.acmicpc.net/problem/17429
[ 문제 요약 ]
- 트리가 주어지고, 아래 6가지 명령어를 실행합니다.
- 1 X V : 금고 X의 서브 트리에 있는 모든 금고에 V 원을 더합니다. (1 ≤ X ≤ N, 1 ≤ V ≤ 10^9)
- 2 X Y V : 금고 X부터 금고 Y까지의 경로에 있는 모든 금고에 V 원을 더합니다. 단, 경로는 경계를 포함합니다. (1 ≤ X, Y ≤ N, 1 ≤ V ≤ 10^9)
- 3 X V : 금고 X의 서브 트리에 있는 모든 금고의 돈을 V 배합니다. (1 ≤ X ≤ N, 0 ≤ V ≤ 10^9)
- 4 X Y V : 금고 X부터 금고 Y까지의 경로에 있는 모든 금고의 돈을 V 배합니다. 단, 경로는 경계를 포함합니다. (1 ≤ X, Y ≤ N, 0 ≤ V ≤ 10^9)
- 5 X : 금고 X의 서브 트리에 있는 모든 금고의 돈을 합한 값을 출력합니다. (1 ≤ X ≤ N)
- 6 X Y : 금고 X부터 금고 Y까지의 경로에 있는 모든 금고의 돈을 합한 값을 출력합니다. 단, 경로는 경계를 포함합니다. (1 ≤ X, Y ≤ N)
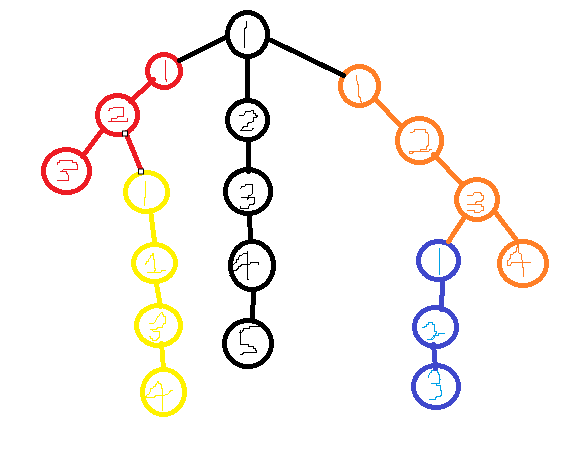
[ 테스트 케이스 설명 ]
5 10 // 노드 수(1<=500,000), 쿠리 수(1<=100,000)
2 4 // N-1개 줄에 간선 정보
4 3
5 4
2 1
3 1 82 // 3 X V : 금고 X의 서브트리에 있는 모든 금고의 돈을 V배(V=10^9)
6 3 5 // 6 X Y : 금고 X부터 금고 Y까지 경로에 있는 모든 금고의 돈을 합하여 출력
2 2 5 45 // 2 X Y V : 금고 X부터 Y까지 경로의 모든 금고에 V를 더함
2 3 2 70
6 3 5
5 3 // 5 X : 금고 X의 서브트리에 있는 모든 금고의 돈을 합한 값을 출력
4 2 1 47
1 1 95 // 1 X V : 금고 X의 서브트리에 있는 모든 금고에 V원을 더함
6 3 2
4 5 1 38 // 4 X Y V : 금고 X부터 금고 Y까지 경로에 있는 모든 금고의 돈을 V배함
// 답( 2^32로 나눈 나머지 출력 )
0
230
70
5875
[ 알고리즘 분류 ]
- 자료 구조, 트리, 느리게 갱신되는 세그먼트 트리
- 오일러 경로 테크닉, heavy-light 분할
[ 문제 해설 ]
이 문제는 여러 가지 알고리즘을 복합적으로 구현 해야 제한 시간 내에 통과하는 코드를 만들 수 있습니다.
사용되는 알고리즘은 아래와 같습니다.
[ HDL + 오일러 경로 테크닉 + 느리게 갱신되는 세그먼트 트리 ]
먼저 HLD와 오일러 경로 테크닉 알고리즘을 이용해 트리 정보를 세그먼트 트리 인덱스에 대응되도록 할 수 있습니다.
그리고 특정 노드에 값 V를 더하거나, 곱하는 것은 느리게 갱신되는 세그먼트 트리를 이용합니다.
곱하고 더하는 것을 lazy로 전파하는 것에 대해 공식이 있는데 이에 관한 문제 해설이 아래 13925문제에 되어있으니 참고하셔도 됩니다. lazy 배열의 더할 숫자와 곱할 숫자를 따로 관리하는 것이 핵심입니다.
https://kyjdummy.tistory.com/15
BOJ 백준 13925 수열과 쿼리 13
문제 : https://www.acmicpc.net/problem/13925 [ 문제 요약 ]배열의 초깃값이 주어지고, 명령어가 주어졌을 때, 명령어에 따라 배열의 값을 수정하는 것입니다.명령어 코드가 1일 때는 x, y 범위의 모든 값에
kyjdummy.tistory.com
문제에서 출력은 2^32로 나눈 나머지를 출력하라고 해서 무턱대고 MOD를 2^32로 잡고 나머지 연산을 하면 틀립니다.
그 이유는 컴퓨터 자체가 32비트를 쓴다고 했기 때문에, 32비트 이상은 버려야 합니다.
이를 표현하기 위해 모든 결괏값에 (1<<32) - 1한 값을 AND 비트 연산(&) 해야 그 이상은 모두 버려지게 되어 AC입니다.
이 부분을 지키지 않으면 틀립니다.
코드에서 세그먼트 트리 부분만 볼 수 있게 클래스로 분리했습니다.
[ 정답 코드 ]
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Collections;
import java.util.StringTokenizer;
class Main{
static final long MOD = (1L<<32) - 1;
static int N, Q;
static int idx; // 노드번호 -> 트리번호로 바꿀 순차증가 인덱스
static int [] treeIdx; // 노드번호 -> 트리번호 정보 저장할 배열
static int [] chainHead; // 각 체인의 head번호
static int [] chainLevel; // 각 체인의 level
static int [] chainParent; // 이전 체인으로 바로 점프할 수 있도록 노드마다 이전 체인의 정보를 담을 배열
static int [][] range; // 각 노드의 서브트리 범위를 알기 위한 배열( 오일러 경로 테크닉 )
static SegmentTree seg; // 세그먼트 트리 연산을 진행할 세그먼트 트리 클래스
static ArrayList<Integer>[] adNode;// 인접 노드 정보를 담을 리스트 배열
public static void main(String[] args)throws Exception{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
StringBuilder sb = new StringBuilder();
N = Integer.parseInt(st.nextToken());
Q = Integer.parseInt(st.nextToken());
treeIdx = new int[N + 1];
chainHead = new int[N + 1];
chainLevel = new int[N + 1];
chainParent = new int[N + 1];
range = new int[N + 1][2];
adNode = new ArrayList[N + 1];
seg = new SegmentTree(N, MOD);
for(int i=0; i<=N; i++)
adNode[i] = new ArrayList<>();
for(int i=1; i<N; i++)
{
st = new StringTokenizer(br.readLine());
int n1 = Integer.parseInt(st.nextToken());
int n2 = Integer.parseInt(st.nextToken());
adNode[n1].add(n2);
adNode[n2].add(n1);
}
// setSize : 이 함수에서 heavy한 자식노드를 인접 노드의 가장 앞쪽으로 옮긴다.
setSize(1, 0, new int[N + 1]);
chainParent[1] = 1;
chainHead[1] = 1; // 1번 노드의 헤드는 자기 자신
// setHLD : 이 함수에서 HLD를 위한 chain정보를 입력하며 동시에 노드당 서브트리의 범위 + 노드 -> 세그먼트 트리 인덱스 번호를 저장
setHLD(1, 0, 1);
int op, x, y, v;
while(Q-->0)
{
st = new StringTokenizer(br.readLine());
op = Integer.parseInt(st.nextToken());
switch(op)
{
case 1: // 1 X V : 금고 X의 서브트리에 있는 모든 금고에 V원을 더함
x = Integer.parseInt(st.nextToken());
v = Integer.parseInt(st.nextToken());
seg.update(1, 1, N, range[x][0], range[x][1], v, true);
break;
case 2: // 2 X Y V : 금고 X부터 Y까지 경로의 모든 금고에 V를 더함
x = Integer.parseInt(st.nextToken());
y = Integer.parseInt(st.nextToken());
v = Integer.parseInt(st.nextToken());
updatePath(x, y, v, true);
break;
case 3: // 3 X V : 금고 X의 서브트리에 있는 모든 금고의 돈을 V배(V=10^9)
x = Integer.parseInt(st.nextToken());
v = Integer.parseInt(st.nextToken());
seg.update(1, 1, N, range[x][0], range[x][1], v, false);
break;
case 4: // 4 X Y V : 금고 X부터 금고 Y까지 경로에 있는 모든 금고의 돈을 V배함
x = Integer.parseInt(st.nextToken());
y = Integer.parseInt(st.nextToken());
v = Integer.parseInt(st.nextToken());
updatePath(x, y, v, false);
break;
case 5: // 5 X : 금고 X의 서브트리에 있는 모든 금고의 돈을 합한 값을 출력
x = Integer.parseInt(st.nextToken());
sb.append( seg.query(1, 1, N, range[x][0], range[x][1])).append('\n');
break;
case 6: // 6 X Y : 금고 X부터 금고 Y까지 경로에 있는 모든 금고의 돈을 합하여 출력
x = Integer.parseInt(st.nextToken());
y = Integer.parseInt(st.nextToken());
sb.append( queryPath(x, y) ).append('\n');
break;
}
}
System.out.print(sb);
}
public static void updatePath(int x, int y, int v, boolean isPlus)
{
while(chainHead[x] != chainHead[y])
{
if(chainLevel[x] > chainLevel[y])
{
int tmp = x;
x = y;
y = tmp;
}
seg.update(1, 1, N, treeIdx[chainHead[y]], treeIdx[y], v, isPlus);
y = chainParent[y];
}
if(treeIdx[x] > treeIdx[y])
{
int tmp = x;
x = y;
y = tmp;
}
seg.update(1, 1, N, treeIdx[x], treeIdx[y], v, isPlus);
}
public static long queryPath(int x, int y)
{
long sum = 0;
// 금고 X부터 금고 Y까지 경로에 있는 모든 금고의 돈을 합하여 출력
while(chainHead[x] != chainHead[y])
{
if(chainLevel[x] > chainLevel[y])
{
int tmp = x;
x = y;
y = tmp;
}
sum += seg.query(1, 1, N, treeIdx[chainHead[y]], treeIdx[y]);
sum &= MOD;
y = chainParent[y];
}
if(treeIdx[x] > treeIdx[y])
{
int tmp = x;
x = y;
y = tmp;
}
sum += seg.query(1, 1, N, treeIdx[x], treeIdx[y]);
return sum & MOD;
}
public static void setHLD(int nowNode, int parentNode, int level) {
++idx;
chainLevel[nowNode] = level;
treeIdx[nowNode] = idx; // 노드번호 -> 세그먼트 트리 인덱스
range[nowNode][0] = idx; // 서브 트리의 시작 범위
for(int i=0; i<adNode[nowNode].size(); i++)
{
int next = adNode[nowNode].get(i);
if(next == parentNode)
continue;
if(i == 0) // heavy 노드일 경우, 체인 유지
{
chainHead[next] = chainHead[nowNode];
chainParent[next] = chainParent[nowNode];
setHLD(next, nowNode, level);
}
else // light 노드일 경우 새로운 체인 시작
{
chainHead[next] = next; // 체인의 head는 자기자신
chainParent[next] = nowNode; // 이전 체인으로 바로 점프할 수 있게 이전 체인의 특정 노드 입력
setHLD(next, nowNode, level + 1);// 새 체인 시작시 레벨 증가
}
}
range[nowNode][1] = idx; // 서브 트리의 마지막 인덱스
}
public static void setSize(int nowNode, int parentNode, int[] size) {
int heavySize = 0;
int heavyIdx = 0;
size[nowNode] = 1;
for(int i=0; i<adNode[nowNode].size(); i++)
{
int next = adNode[nowNode].get(i);
if(next == parentNode)
continue;
setSize(next, nowNode, size);
size[nowNode] += size[next];
if(heavySize < size[next])
{
heavySize = size[next];
heavyIdx = i;
}
}
if(adNode[nowNode].size() > 0)
Collections.swap(adNode[nowNode], 0, heavyIdx);
}
}
class SegmentTree{
long MOD;
long N;
long [] tree;
Node [] lazy;
SegmentTree(int n, long MOD){
this.N = n;
this.MOD = MOD;
this.tree = new long[n * 4];
this.lazy = new Node[n * 4];
for(int i=0; i<n*4; i++)
lazy[i] = new Node(0, 1);
}
public void propagate(int treeNode, int s, int e) {
if(lazy[treeNode].sum != 0 || lazy[treeNode].mul != 1)
{
tree[treeNode] *= lazy[treeNode].mul;
tree[treeNode] &= MOD;
tree[treeNode] += (e - s + 1) * lazy[treeNode].sum;
tree[treeNode] &= MOD;
if(s != e)
{
int left = treeNode << 1;
int right= treeNode << 1 | 1;
lazy[left].mul = (lazy[left].mul * lazy[treeNode].mul) & MOD;
lazy[right].mul = (lazy[right].mul * lazy[treeNode].mul) & MOD;
lazy[left].sum *= lazy[treeNode].mul;
lazy[left].sum &= MOD;
lazy[left].sum += lazy[treeNode].sum;
lazy[left].sum &= MOD;
lazy[right].sum *= lazy[treeNode].mul;
lazy[right].sum &= MOD;
lazy[right].sum += lazy[treeNode].sum;
lazy[right].sum &= MOD;
}
lazy[treeNode].sum = 0;
lazy[treeNode].mul = 1;
}
}
public void update(int treeNode, int s, int e, int left, int right, int value, boolean isPlus) {
propagate(treeNode, s, e);
if(e < left || right < s)
return;
if(left <= s && e <= right)
{
if(isPlus)
{
lazy[treeNode].sum = value;
lazy[treeNode].mul = 1;
}
else
{
lazy[treeNode].sum = 0;
lazy[treeNode].mul = value;
}
propagate(treeNode, s, e);
return;
}
int mid = (s + e) >> 1;
update(treeNode << 1, s, mid, left, right, value, isPlus);
update(treeNode << 1 | 1, mid + 1, e, left, right, value, isPlus);
tree[treeNode] = (tree[treeNode << 1] + tree[treeNode << 1 | 1]) & MOD;
}
public long query(int treeNode, int s, int e, int left, int right) {
propagate(treeNode, s, e);
if(e < left || right < s)
return 0;
if(left <= s && e <= right)
return tree[treeNode];
int mid = (s + e) >> 1;
long l = query(treeNode << 1, s, mid, left, right);
long r = query(treeNode << 1 | 1, mid + 1, e, left, right);
return (l + r) & MOD;
}
}
class Node{
long sum, mul;
Node(long s, long m){
sum = s;
mul = m;
}
}'알고리즘 > HLD(Heavy-Light Decomposition)' 카테고리의 다른 글
| BOJ 백준 2927 남극 탐험 (1) | 2025.04.30 |
|---|---|
| BOJ 백준 13038 Tree (0) | 2025.04.29 |
| BOJ 백준 30092 슥삭슥삭 나무자르기 (1) | 2025.04.28 |
| BOJ 백준 16453 Linhas de Metrô (0) | 2025.04.28 |
| BOJ 백준 31234 대역폭 관리 (0) | 2025.04.27 |