문제 : https://www.acmicpc.net/problem/13510
[ 문제 요약 ]
- N 개의 노드와 N - 1개의 간선이 주어지며 2가지 명령어가 임의로 주어집니다.
- 1 i c : i 번 간선의 비용을 c로 변경
- 2 u v : u에서 v로 가는 단순 경로에 존재하는 간선 비용 중 가장 큰 것을 출력합니다.
- 2번 입력이 주어질 때마다 두 노드 사이 가장 큰 간선 비용을 한 줄에 하나씩 출력합니다.
[ 테스트 케이스 설명 ]
3 // 정점 수(2<=100,000)
1 2 1 // N-1개 줄에 i번 간선이 연결하는 두 정점 번호 u, v와 비용 w(1<=1,000,000)가 주어짐
2 3 2
3 // 쿼리 개수 Q(1<=100,000)
2 1 2
1 1 3 // 1 i c : i번 간선의 비용을 c로 바꾼다.
2 1 2 // 2 u v : u에서 v로 가는 단순 경로에 존재하는 비용 중 가장 큰 것을 출력한다.
답
1
3
[ 문제 해설 ]
이 문제에서 노드가 최대 10만 개이고, 조회하는 쿼리 개수가 10만 개 일 수 있으므로
완전 탐색 시 최악의 경우 O(10만^2)으로 시간 초과입니다.
이 문제를 풀기 위해서는 u, v 사이 간선을 완전 탐색이 아니라, 한 번에 찾을 수 있어야 합니다.
이를 위해 HLD( Heavy -Light Decomposition )과 세그먼트 트리 기법을 이용할 것입니다.
HLD는, 트리 위에서 경로 쿼리, 서브 트리 쿼리를 log^2N 시간에 처리할 수 있게 해주는 [트리 분해 기법]입니다.
세그먼트 트리를 이용하기 위해서는 선형 자료구조여야 하는데, 트리는 비선형이기 때문에 트리를 여러 개로 분할해 분할된 구간마다 세그먼트 트리를 이용할 수 있게 하는 기법입니다.
트리를 분할할 때 아무렇게 하는 게 아니라, 가장 무거운 노드(heavy)를 기준으로 트리를 분할합니다. ( 이렇게 하면 쿼리 시 건너야 할 체인 수를 logN으로 한정 지을 수 있는 수학적 이론이 있으나 길어져 생략합니다. )
가장 무거운 노드란 문제에 따라 정의하기 나름이겠으나, 이 문제에서는 자식 노드의 수가 가장 많은 노드를 무거운 노드라고 정의합니다.
트리를 분할할 때 분할되는 그룹 단위를 체인이라고 정의합니다. 분할 후 하나의 트리는 논리적인 여러 개의 체인이 되는 겁니다. 이 체인마다 대응되는 세그먼트 트리의 인덱스가 있게 되는 것입니다.
입력된 간선 정보를 기반으로 연결 리스트를 만들어 놓고,
첫 번째 DFS를 돌면서 자식 노드의 크기를 세고, 자식 노드의 크기가 가장 큰 노드를 알아볼 수 있게 마킹합니다. 여기서 마킹은, 구현에 따라 다르겠지만, 저는 가장 무거운 노드를 연결 리스트상에서 가장 앞으로 옮겼습니다. int형 배열에 별도로 직접 명시해도 되겠으나 구현상 가장 무거운 노드를 앞으로 옮기면 0번째 인덱스가 무거운 노드라는 것을 알 수 있기 때문에 편합니다.
그 후 두 번째 DFS를 돌면서 논리적인 체인 정보들을 입력하며, 이때 각 노드들이 세그먼트 트리에 대응될 인덱스도 세팅합니다.
논리적인 체인 정보들을 알아보기 전에, 해당 체인 정보들이 왜 언제 필요한지, 어떻게 응용되는지 그림을 통해 설명드리겠습니다.
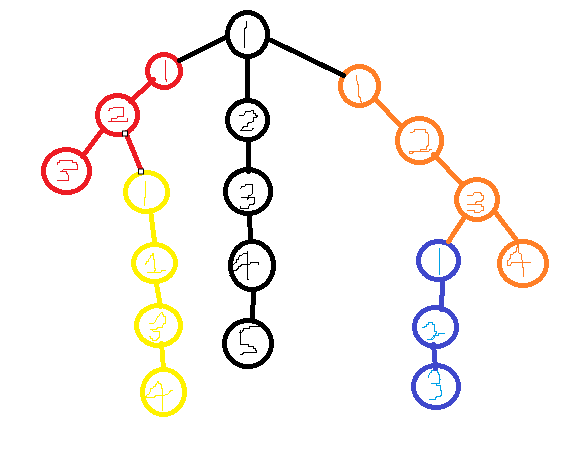
[ 그림 설명 ]
- 하나의 트리를 여러 개의 체인으로 구분한 그림이며, 각 체인의 색깔은 하나의 체인 그룹이라 생각하면 되고, 각 체인마다 세그먼트 트리의 대응되는 인덱스가 순서대로 있습니다.( 그림은 임의로 막 구분 한 것이라 heavy, Light를 따지지 않음 )
- 여기서 노란색 3번 노드에서 파란색 2번 노드까지 경로에서 가장 큰 간선의 값을 찾아야 한다고 칩니다.
- 빠르게 탐색하는 방법은, 노란색 (1,3)까지 최댓값 세그먼트 트리로 빠르게 구하고, 노란색 체인에서 빨간색 체인으로 점프해서 빨간색 (1,2) 사이 최댓값 구하고, 검정 노드도 구하고, 점프해가면서 주황, 파랑도 동일하게 구해줍니다.
- 여기서 하나 알아야 할 것은, 세그먼트 트리에 저장되는 것은 간선 가중치 값이 저장됩니다. 그러나 노드는 A 노드와 B 노드로 2개인데 간선 1개를 저장해야 돼서 어디에 뭘 저장해야 할지 헷갈리는데, 자식 노드에 간선 정보를 저장하면 문제를 풀 수 있습니다. 즉 노란색 1번과 3번 범위를 세그먼트 트리로 max 값을 구한다는 것은, [3번에서 2번가는 간선 + [2번에서 1번가는 간선] + 노란색 1번에서 빨간색 2번으로 가는 간선] 을 구하는 것과 같습니다.
- 이렇게 체인 간 이동을 최소로 빠르고, 정확하게 코드로 구현 하기 위해 몇 가지 정보가 필요합니다.
- 1 ) 처음에 주어지는 트리 노드를 세그먼트 트리에 대응 시킬 인덱스 배열
- 2 ) 현재 나의 체인에서, 다음 체인으로 바로 점프할 수 있도록 다음 체인의 노드 정보를 담는 배열
- 3 ) 현재 나의 체인의 head 노드 번호를 담을 배열 : 예를 들어 노란색 4번 노드는 자기 체인의 head인 1번 노드의 번호를 갖고 있어야 합니다. 그래야 세그먼트 트리에 사용할 범위를 바로 알 수 있습니다.
- 4 ) 해당 체인의 LEVEL 정보를 담을 배열 : LEVEL은 루트가 1이고, 나머지 체인들이 1씩 증가하는 형태를 띠며 LEVEL이 필요한 이유는, 트리 경로 탐색 시 LEVEL이 높은 곳에서부터 낮은 곳으로 올라와야 빠짐없이 정확한 경로 탐색이 가능하기 때문입니다.
위 와 같이 체인 정보들을 구했으면, 노드 두 개가 입력되었을 때 해당 노드 사이의 최대 간선을 쉽게 구할 수 있습니다.
디테일은 코드를 통해 확인 가능합니다.
[ 정답 코드 ]
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Collections;
import java.util.StringTokenizer;
class Main{
static class Node{
int node, value;
Node(int n, int v){
node = n;
value = v;
}
}
static int N, Q;
static int idx; // 입력된 노드 번호를 세그먼트 트리의 인덱스로 전환할 때 증가될 인덱스 값
static int [] tree; // 세그먼트 트리
static int [] treeIdx; // HLD용 : 입력된 노드 번호 -> 세그먼트 트리 인덱스로 변환할 값
static int [] chainHead; // HLD용 : 각 체인 마다의 head 노드, 체인 당 첫번째 노드의 값은 자기 자신이됨
static int [] chainLevel; // HLD용 : 노드가 포함된 체인의 깊이(체인 레벨)
static int [] chainParent; // HLD용 : 내가 속한 체인의 head 노드의 바로 윗노드, 즉, 다음 체인으로 첨프할 때 도착할 노드
static int [][] edge; // 간선 정보 저장
static ArrayList<Node>[] adNode;// 인접 리스트
public static void main(String[] args)throws Exception{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
StringTokenizer st;
N = Integer.parseInt(br.readLine());// 정점 수(2<=100,000)
tree = new int[N * 4];
treeIdx = new int[N + 1];
chainHead = new int[N + 1];
chainLevel = new int[N + 1];
chainParent = new int[N + 1];
edge = new int[N + 1][];
adNode = new ArrayList[N + 1];
for(int i=0; i<=N; i++)
adNode[i] = new ArrayList<>();
for(int i=1; i<N; i++)
{
st = new StringTokenizer(br.readLine());
int node1 = Integer.parseInt(st.nextToken());
int node2 = Integer.parseInt(st.nextToken());
int value = Integer.parseInt(st.nextToken());//비용 w(1<=1,000,000)
adNode[node1].add(new Node(node2, value));
adNode[node2].add(new Node(node1, value));
edge[i] = new int[] {node1, node2};
}
// 이 함수에서는 단순히 HLD를 구현하기 위해 adNode에서 가장 heavy한 자식만 앞으로 옮기는 역할을 합니다.
moveHeavyChildToFront(1, 0, new int[N + 1]);
chainHead[1] = 1; // 1번노드의 헤드는 자기 자신
// 해당 함수에서 HLD를 위한 chain 정보들을 마킹하고, 세그먼트 트리에 간선 가중치를 업데이트 한다.
setHLD(1, 0, 1);
Q = Integer.parseInt(br.readLine());// 쿼리 개수 Q(1<=100,000)
while(Q-->0)
{
st = new StringTokenizer(br.readLine());
int op = Integer.parseInt(st.nextToken());
if(op == 1)// 1 i c : i번 간선의 비용을 j로 바꾼다.
{
int i = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
// 간선 정보는 자식 노드에 저장되어 있으므로, i번째 간선의 2개의 노드를 가져와서
// 세그먼트 트리 노드의 번호로 변경했을 때 큰 값을 찾아 그 값으로 업데이트한다.( 큰값이 자식노드니까 )
// setHLD 함수에서 treeIdx배열 세팅 하는 것을 보면, 자식 노드가 무조건 값이 더 크다.
int segIdx = Math.max(treeIdx[ edge[i][0] ], treeIdx[ edge[i][1] ]);
update(1, 1, N, segIdx, c);
continue;
}
// op가 2인 경우 u, v사이의 간선 중 가중치가 가장 큰 값을 찾는다.
int ans = 0;
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
// 레벨이 같아질 때까지 레벨이 높은 것을 낮게 만들면서 높이를 맞춘다.
if(chainLevel[u] > chainLevel[v]) // v노드가 레벨이 더크게 조정
{
int tmp = v;
v = u;
u = tmp;
}
while(chainLevel[u] != chainLevel[v]) // 레벨이 같아질 때 까지 반복
{
int head = chainHead[v];
// 해당 체인의 head부터, 현재 v노드까지 가장 큰 값을 구해와 ans 갱신
ans = Math.max(ans, query(1, 1, N, treeIdx[head], treeIdx[v]));
v = chainParent[v]; // 레벨이 높은 v를 다음 체인까지 바로 점프 하도록 만든다.
}
// 레벨이 같아졌다면 같은 체인에 속하도록 두 노드의 레벨을 지속적으로 낮춘다.
while(chainHead[v] != chainHead[u])
{
ans = Math.max(ans, query(1, 1, N, treeIdx[chainHead[u]], treeIdx[u]));
ans = Math.max(ans, query(1, 1, N, treeIdx[chainHead[v]], treeIdx[v]));
u = chainParent[u]; // 다음 체인으로 바로 점프
v = chainParent[v]; // 다음 체인으로 바로 점프
}
// 위 연산들을 통해 결국 같은 체인에 속했다면,
// 마지막으로 해당 두 노드간의 부모 자식 노드를 파악한 후, 그 사이의 가장 큰 값을 다시 비교한다.
if(treeIdx[u] > treeIdx[v]) // v를 자식노드로 만든다.
{
int tmp = v;
v = u;
u = tmp;
}
// treeIdx[u] + 1을 하는 이유 :
// 세그먼트 트리에 값을 저장할 때, A가 부모노드이고, B가 자식노드일 때 간선의 가중치를 B위치에 저장했다.
// 그러므로 부모인 자기 자신은 빼주어야 정확한 값을 구해올 수 있다.
ans = Math.max(ans, query(1, 1, N, treeIdx[u] + 1, treeIdx[v]));
sb.append(ans).append('\n');
}
System.out.print(sb);
}
static void setHLD(int nowNode, int parentNode, int level) {
treeIdx[nowNode] = ++idx;
chainLevel[nowNode] = level;
for(int i=0; i<adNode[nowNode].size(); i++)
{
Node now = adNode[nowNode].get(i);
if(now.node == parentNode)
continue;
if(i == 0) // heavy일 경우, 기존 데이터들 그대로 이어짐
{
chainHead[now.node] = chainHead[nowNode];
chainParent[now.node] = chainParent[nowNode];
setHLD(now.node, nowNode, level); // heavy는 level이 그대로 이어진다.
}
else // 새로운 체인 시작
{
chainHead[now.node] = now.node; // 해당 체인의 시작은 자기자신
chainParent[now.node] = nowNode; // 새 체인 시작시 now.node는 nowNode로 바로 점프할 수 있게 저장
setHLD(now.node, nowNode, level + 1); // 새 체인 시작시 레벨 증가
}
// now객체의 모든 연산이 끝난 후, 해당 노드 번호를 이용해 세그먼트 트리에 간선 값을 업데이트한다.
// 부모노드가 A, 자식노드 B라 할 때, 노드는 2개지만 간선은 하나기 때문에 간선 정보는 자식노드에 저장한다.
// 그래서 현재 함수에서 nowNode(부모노드)에 저장하는것이 아닌, 자식 노드인 now.node에 간선 정보를 저장한다.
update(1, 1, N, treeIdx[now.node], now.value);
}
}
static void moveHeavyChildToFront(int nowNode, int parentNode, int[] size) {
int heavySize = 0;
int heavyIdx = 0;
size[nowNode] = 1;
for(int i=0; i<adNode[nowNode].size(); i++)
{
Node now = adNode[nowNode].get(i);
if(now.node == parentNode) // 부모노드면 스킵
continue;
moveHeavyChildToFront(now.node, nowNode, size);
size[nowNode] += size[now.node]; // 자기 자식의 크기를 자기크기에 합산
if(heavySize < size[now.node]) // 자식 노드 크기 중 큰 것의 idx를 갱신해나감
{
heavySize = size[now.node];
heavyIdx = i;
}
}
// 0번째 인덱스에 가장 무거은 노드를 놓아 추후 있을 연산들을 단순하게 한다.
Collections.swap(adNode[nowNode], 0, heavyIdx);
}
static void update(int treeNode, int s, int e, int targetIdx, int value) {
if(e < targetIdx || targetIdx < s)
return;
if(s == e)
{
tree[treeNode] = value;
return;
}
int mid = (s + e) >> 1;
update(treeNode << 1, s, mid, targetIdx, value);
update(treeNode << 1 | 1, mid + 1, e, targetIdx, value);
tree[treeNode] = Math.max(tree[treeNode << 1], tree[treeNode << 1 | 1]);
}
static int query(int treeNode, int s, int e, int left, int right) {
if(e < left || right < s)
return 0;
if(left<=s && e<=right)
return tree[treeNode];
int mid = (s + e) >> 1;
int l = query(treeNode << 1, s, mid, left, right);
int r = query(treeNode << 1 | 1, mid + 1, e, left, right);
return Math.max(l,r);
}
}
'알고리즘 > HLD(Heavy-Light Decomposition)' 카테고리의 다른 글
| BOJ 백준 16453 Linhas de Metrô (0) | 2025.04.28 |
|---|---|
| BOJ 백준 31234 대역폭 관리 (0) | 2025.04.27 |
| BOJ 백준 17033 Cow Land (1) | 2025.04.26 |
| BOJ 백준 13309 트리 (0) | 2025.04.26 |
| BOJ 백준 13512 트리와 쿼리 3 (0) | 2025.04.26 |
